পরিবহনে বিজ্ঞান/ট্রাফিক প্রবাহ

পর্তুগালে ট্রাফিক জ্যাম

ট্রাফিক প্রবাহ হচ্ছে দুটি পয়েন্টের মধ্যে পৃথক ড্রাইভার এবং যানবাহনের চলাচল এবং তারা একে অপরের সাথে যে মিথস্ক্রিয়া করে তার অধ্যয়ন। দুর্ভাগ্যবশত, ট্রাফিক প্রবাহ অধ্যয়ন করা কঠিন কারণ চালকের আচরণ শতভাগ নিশ্চয়তার সাথে ভবিষ্যদ্বাণী করা যায় না। সৌভাগ্যবশত, চালকরা যুক্তিসঙ্গতভাবে সামঞ্জস্যপূর্ণ পরিসরের মধ্যে আচরণ করে; এইভাবে, ট্র্যাফিক স্ট্রিমগুলির কিছু যুক্তিসঙ্গত সামঞ্জস্য থাকে এবং মোটামুটিভাবে গাণিতিকভাবে উপস্থাপন করা যেতে পারে। ট্র্যাফিক প্রবাহকে আরও ভালভাবে উপস্থাপন করার জন্য, তিনটি প্রধান বৈশিষ্ট্যের মধ্যে সম্পর্ক স্থাপন করা হয়েছে: (১) প্রবাহ, (২) ঘনত্ব এবং (৩) বেগ। এই সম্পর্কগুলি রাস্তার সুবিধাগুলির পরিকল্পনা, নকশা এবং পরিচালনায় সহায়তা করে।

ট্রাফিক প্রবাহ তত্ত্ব

টাইম-স্পেস ডায়াগ্রাম

টাইম-স্পেস ডায়াগ্রাম সময় এবং স্থানের সাথে যানবাহনের গতিপথ দেখায়

ট্রাফিক ইঞ্জিনিয়াররা একটি নির্দিষ্ট সময়ে একটি নির্দিষ্ট গাড়ির অবস্থান একটি টাইম-স্পেস ডায়াগ্রামের মাধ্যমে উপস্থাপন করে। এই দ্বি-মাত্রিক চিত্রটি একটি নির্দিষ্ট উৎস থেকে একটি নির্দিষ্ট গন্তব্যে যাওয়ার সময় একটি গাড়ির গতিপথ দেখায়। একটি ডায়াগ্রামে একাধিক যানবাহনকে উপস্থাপন করা যেতে পারে এবং এইভাবে, নির্দিষ্ট বৈশিষ্ট্যগুলি, যেমন একটি নির্দিষ্ট সময়ের জন্য একটি নির্দিষ্ট সাইটে প্রবাহ, নির্ধারণ করা যেতে পারে।

প্রবাহ এবং ঘনত্ব

প্রবাহ (q) = যে হারে যানবাহনগুলি একটি নির্দিষ্ট পয়েন্ট অতিক্রম করে (ঘন্টা প্রতি যানবাহন) , $t_{measured}$ = গড় পরিমাপ সময় অগ্রগতি

$q={\frac {3600N}{t_{measured}}}\,\!$

ঘনত্ব (কেন্দ্রীকরণ) (k) = রাস্তার একটি প্রসারিত (L) উপর যানবাহনের সংখ্যা (N) (প্রতি কিলোমিটার যানবাহনের ইউনিটে)

$k={\frac {N}{L}}\,\!$

যেখানে:

• $N$ = $L$ দৈর্ঘ্যের একটি হাইওয়ে অংশ দখলকারী যানবাহনের সংখ্যা
• $q$ = সমান ঘণ্টায় প্রবাহ
• $L$ = রাস্তার দৈর্ঘ্য
• $k$ = ঘনত্ব

গতি

ট্র্যাফিকের গতি পরিমাপ যতটা স্পষ্ট মনে হয় ততটা নয়; আমরা সময়ের সাথে বা স্থান ধরে পৃথক যানবাহনের গতির পরিমাপ গড় করতে পারি এবং প্রতিটি সামান্য ভিন্ন ফলাফল দেয়।

সময় মাধ্যম গতি

সময় মাধ্যম গতি (${\overline {v_{t}}}\,\!$) = একটি বিন্দু অতিক্রমকারী যানবাহনের গতির গাণিতিক গড়

${\overline {v_{t}}}={\frac {1}{N}}\sum \limits _{n=1}^{N}{v_{n}}\,\!$

ব্যবধান মাধ্যম গতি

ব্যবধান মাধ্যম গতি (${\overline {v_{s}}}\,\!$) নির্দিষ্ট সময়ের মধ্যে একটি বিন্দু অতিক্রম করার গতির সুরেলা গড় হিসাবে সংজ্ঞায়িত করা হয়। এটি রাস্তার দৈর্ঘ্যের গড় গতির সমান।

${\overline {v_{s}}}={\frac {N}{\sum \limits _{n=1}^{N}{\frac {1}{v_{n}}}}}\,\!$

সময় এবং স্থান সম্পর্কিত মাধ্যম গতি

মনে রাখবেন যে সময়ের মাধ্যম গতি হল একটি বিন্দুর পরের গড় গতি যা স্থান থেকে পৃথক হিসাবে মাধ্যম গতি যা একটি দৈর্ঘ্য বরাবর গড় গতি।

দুটি গতি যেমন সম্পর্কিত

${\overline {v_{t}}}={\overline {v_{s}}}+{\frac {\sigma _{s}^{2}}{\overline {v_{s}}}}\,\!$

সময়ের অর্থ স্থানের চেয়ে বেশি গতি মাধ্যম গতি, তবে পার্থক্যগুলি যানবাহনের গতির মধ্যে পরিবর্তনশীলতার পরিমাণের সাথে পরিবর্তিত হয়। উচ্চ গতিতে (মুক্ত প্রবাহ), পার্থক্যগুলি ছোটখাটো, যেখানে ঘনবসতিপূর্ণ সময়ে, সেখানে ফ্যাক্টর ২ ভিন্ন হতে পারে।

অগ্রগমন

নিচে নেটটো গ্যাপের (নেট শব্দের ইতালীয়) বিপরীতে ব্রুটটো গ্যাপ (আসেলা, স্থূলের জন্য ইতালীয়) এর সংজ্ঞা দেয়া হয়েছে।। যখন নেটটো গ্যাপ একটি গাড়ির পিছনের বাম্পার এবং পরের বাম্পারটির মধ্যে দূরত্ব বা সময় দেয়৷

সময় অগ্রগমন

সময় অগ্রগমন ($h_{t}\,\!$) = মহাসড়কের একটি বিন্দুতে একটি গাড়ির সামনে আসার সময় এবং পরবর্তী গাড়ির সামনের একই পয়েন্টে আসার সময়ের মধ্যে পার্থক্য (সেকেন্ডে)

গড় সময় অগ্রগমন (${\overline {h_{t}}}\,\!$) = প্রতি ইউনিট দূরত্ব প্রতি গড় ভ্রমণ সময় * গড় ব্যবধান অগ্রগতি

${\overline {h_{t}}}={\overline {t}}*{\overline {h_{s}}}\,\!$

ব্যবধান অগ্রগমন

ব্যবধান অগ্রগমন ($h_{s}$) = একটি গাড়ির সামনের এবং পরবর্তী গাড়ির সামনের ব্যবধানের মধ্যে পার্থক্য (মিটারে)

গড় ব্যবধান অগ্রগমন (${\overline {h_{s}}}\,\!$)= ব্যবধান গড় গতি * গড় সময় অগ্রগতি

${\overline {h_{s}}}={\overline {v_{s}}}*{\overline {h_{t}}}\,\!$

উল্লেখ্য যে ঘনত্ব এবং ব্যবধান অগ্রগমন সম্পর্কিত:

$k={\frac {1}{\overline {h_{s}}}}\,\!$

ট্রাফিক প্রবাহের মৌলিক চিত্র

ট্র্যাফিকের ঐতিহ্যগত মৌলিক চিত্র

১লা নভেম্বর ২০০০-এ ডিটেক্টর ৬৮৮ (মিনিয়াপলিসের ৪৯তম/৫৩তম অ্যাভিনিউতে আই-৯৪) ঘনত্ব অনুসারে প্রবাহ পরিবর্তিত হয়

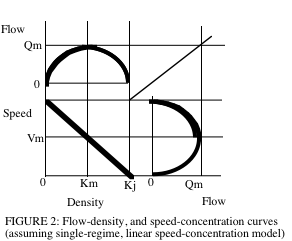
প্রবাহ, ঘনত্ব এবং ব্যবধান গড় গতির পরিবর্তনশীলগুলি সংজ্ঞাগতভাবে সম্পর্কিত:

$q=k{\overline {v_{s}}}\,\!$

ঐতিহ্যগত মডেল (প্যারাবোলিক)

ঐতিহ্যগত মৌলিক চিত্রের বৈশিষ্ট্য।

• মহাসড়কে যখন ঘনত্ব শূন্য হয়, তখন প্রবাহও শূন্য হয় কারণ মহাসড়কে কোনো যানবাহন নেই।
• ঘনত্ব বাড়ার সাথে সাথে প্রবাহ বৃদ্ধি পায়
• যখন ঘনত্ব সর্বাধিক যানজট ঘনত্বে পৌঁছায় ($k_{j}$), প্রবাহ শূন্য হতে হবে কারণ যানবাহন শেষ থেকে শেষ লাইনে থাকবে
• প্রবাহ সর্বোচ্চ মান পর্যন্ত বৃদ্ধি পাবে ($q_{m}$), সেই বিন্দুর বাইরে ঘনত্ব বৃদ্ধির ফলে প্রবাহ হ্রাস পায়।
• গতি হল ব্যবধান মানে গতি।
• ঘনত্বে = 0, গতি প্রবাহমুক্ত ($v_{f}$). প্রবাহ বক্ররেখার উপরের অর্ধেকটি যানজটবিহীন, নীচের অর্ধেকটি যানজটপূর্ণ।.
• প্রবাহের ঘনত্ব বক্ররেখার ঢাল গতি দেয়। উত্থান/চালা = প্রবাহ/ঘনত্ব = যানবাহন প্রতি ঘন্টা/ যানবাহন প্রতি কিমি = কিমি/ঘন্টা।

পর্যবেক্ষণ (ত্রিভুজাকার বা কাটা ত্রিভুজাকার)

প্রকৃত ট্র্যাফিক ডেটা প্রায়শই আদর্শ মডেলের পরামর্শের চেয়ে অনেক বেশি শোরগোল করে। যাইহোক, আমরা যা দেখতে পাই তা হল যে ঘনত্ব বৃদ্ধির সাথে সাথে গতি একটি বিন্দুতে (ক্ষমতা) অপরিবর্তিত থাকে এবং তারপরে যদি এটি ডাউনস্ট্রিম ট্র্যাফিক (সারি স্পিলব্যাক) দ্বারা প্রভাবিত হয় তবে এটি হ্রাস পেতে শুরু করে। একটি একক লিঙ্কের জন্য, প্রবাহ এবং ঘনত্বের মধ্যে সম্পর্ক এইভাবে প্যারাবোলিকের চেয়ে বেশি ত্রিভুজাকার। যখন আমরা একাধিক লিঙ্ক একসাথে একত্রিত করি (যেমন একটি নেটওয়ার্ক), তখন আমরা আরও প্যারাবোলিক আকৃতি দেখতে পাই।

মাইক্রোস্কোপিক এবং ম্যাক্রোস্কোপিক মডেল

ট্র্যাফিক প্রবাহ বর্ণনাকারী মডেল দুটি বিভাগে শ্রেণীবদ্ধ করা যেতে পারে: মাইক্রোস্কোপিক এবং ম্যাক্রোস্কোপিক। আদর্শভাবে, ম্যাক্রোস্কোপিক মডেলগুলি মাইক্রোস্কোপিক মডেলগুলিতে দেখা আচরণের সমষ্টি।

একটি মাইক্রোস্কোপিক মৌলিক ডায়াগ্রামে ট্র্যাফিক পর্যায়গুলি (কাটা ত্রিভুজাকার)

সারিবদ্ধ ক্রমবর্ধমান ইনপুট-আউটপুট (নিওয়েল) ডায়াগ্রামে ট্র্যাফিক পর্যায়গুলি

মাইক্রোস্কোপিক মডেল

মাইক্রোস্কোপিক মডেলগুলি গাড়ির নিম্নলিখিত আচরণের পূর্বাভাস দেয় (তাদের গতি এবং অবস্থানের পরিবর্তন) নেতৃস্থানীয় গাড়ির আচরণের একটি ফাংশন হিসাবে।

ম্যাক্রোস্কোপিক মডেল

ম্যাক্রোস্কোপিক ট্রাফিক প্রবাহ তত্ত্ব ট্রাফিক প্রবাহ, চলমান গতি এবং ঘনত্ব সম্পর্কিত। একটি স্রোতে ট্র্যাফিককে সাদৃশ্যপূর্ণ করে, এটি মূলত সীমিত অ্যাক্সেস পথে জন্য তৈরি করা হয়েছে (লিউজবাখ ১৯৮৮). প্রবাহ, ঘনত্ব, এবং গতির মধ্যে মৌলিক সম্পর্কটি হল "q = kv" (প্রবাহ [q] সমান ঘনত্ব [k] গুণ গতি [v])। এই সমীকরণটি মৌলিক ডায়াগ্রামের মাধ্যমে চিত্রিত হয়। অনেক পরীক্ষামূলক অধ্যয়ন বিভিন্ন সম্পর্কের পরিমাণ নির্ধারণ করেছে, যেমন প্রবাহ বনাম গতি (q বনাম v), প্রবাহ বনাম ঘনত্ব (q বনাম k), এবং ঘনত্ব বনাম গতি (k বনাম v)। এই গবেষণাগুলির মাধ্যমে গুরুত্বপূর্ণ প্যারামিটারের পরিমাপ এবং কার্যকরী রূপগুলি আরও পরিশীলিত করা হয়েছে (Gerlough and Huber 1975, Pensaud and Hurdle 1991; Ross 1991; Hall, Hurdle and Banks 1992; Banks 1992; Gilchrist and Hall 1992; Disbro and Frame 1992)।

সবচেয়ে ব্যাপকভাবে ব্যবহৃত মডেলটি হল গ্রিনশীল্ডস মডেল। এই মডেলটি ধরে নেয় যে গতি এবং ঘনত্বের মধ্যে সম্পর্কটি রৈখিক। উচ্চ-ক্ষমতা সম্পন্ন কম্পিউটারের আবির্ভাবের পূর্বে, যা মাইক্রোস্কোপিক মডেল ব্যবহারের অনুমতি দেয়, তখন এই মডেলটিই সবচেয়ে উপযুক্ত ছিল। প্রবাহ এবং ঘনত্বের মতো ম্যাক্রোস্কোপিক বৈশিষ্ট্যগুলি হল ব্যক্তিগত (মাইক্রোস্কোপিক) সিদ্ধান্তের ফলাফল। তবে, এই মাইক্রোস্কোপিক সিদ্ধান্ত গ্রহণকারীরা তাদের চারপাশের পরিবেশ, অর্থাৎ ট্রাফিকের ম্যাক্রোস্কোপিক বৈশিষ্ট্য দ্বারা প্রভাবিত হয়।

পরিবহন প্রবাহ তত্ত্ববিদরা যখন যানবাহন চলাচলের কথা বলেন, তখন তারা এটিকে পানির মতো তরল পদার্থের ন্যায় বিবেচনা করেন। অন্যদিকে, সারিবদ্ধ বিশ্লেষণ যানবাহন চলাচলকে পৃথক পৃথক কণার সমষ্টি হিসেবে ধারণ করে। এই দুটি উপস্থাপনা একে অপরের সাথে বিরোধপূর্ণ নয়। ডানদিকের চিত্রগুলিতে মৌলিক ডায়াগ্রাম এবং সারিবদ্ধ ইনপুট-আউটপুট ডায়াগ্রামের একই চারটি পর্যায় তুলে ধরা হয়েছে। পরবর্তী অধ্যায়ে এ বিষয়ে আরও বিস্তারিত আলোচনা করা হবে।

উদাহরণসমূহ

উদাহরণ ১: সময়-মাধ্যম এবং ব্যবধান-গড় গতি

TProblem

সমস্যা:

নিরীক্ষা করা পাঁচটি গতিবেগ দেওয়া হয়েছে (৫০ কিমি/ঘণ্টা, ৩৫ কিমি/ঘণ্টা, ৪৫ কিমি/ঘণ্টা, ২০ কিমি/ঘণ্টা, এবং ৫০ কিমি/ঘণ্টা)। এই গতিবেগগুলি থেকে সময়-মাধ্যম গতি এবং স্থান-মাধ্যম গতি কীভাবে নির্ণয় করবেন?

Example

সমাধান:

সময়-মাধ্যম গতি:

${\overline {v_{t}}}={\frac {1}{5}}(60+35+45+20+50)=42\,\!$

স্থান-মাধ্যম গতি:

${\overline {v_{s}}}={\frac {N}{\sum \limits _{n=1}^{N}{\frac {1}{v_{n}}}}}={\frac {5}{{\frac {1}{60}}+{\frac {1}{35}}+{\frac {1}{45}}+{\frac {1}{20}}+{\frac {1}{50}}}}=36.37\,\!$

সময়-মাধ্যম গতি হল ৪২ কিমি/ঘণ্টা এবং স্থান-মাধ্যম গতি হল ৩৬.৩৭ কিমি/ঘণ্টা।

উদাহরণ ২: ট্রাফিক প্রবাহের বৈশিষ্ট্য নির্ণয়

TProblem

সমস্যা:

দেওয়া আছে, ১ মিনিটে একটি নির্দিষ্ট স্থান দিয়ে ৪০টি যান চলাচল করে এবং সেগুলো ১ কিলোমিটার দীর্ঘ রাস্তা অতিক্রম করে। এই তথ্য থেকে আমরা কীভাবে প্রবাহ, ঘনত্ব, এবং সময় ব্যবধান নির্ণয় করব?

Example

সমাধান:

প্রবাহ এবং ঘনত্ব গণনা:

$q={\frac {3600(40)}{60s}}=2400veh/hr\,\!$

$k={\frac {40}{1}}=40veh/km\,\!$

স্থান-মাধ্যম গতি খুঁজে পাই,

$q=k{\overline {v_{s}}}=2400=40{\overline {v_{s}}}\,\!$

${\overline {v_{s}}}=60km/hr\,\!$

স্থানের অগ্রগমন গণনা:

$k=40={\frac {1}{\overline {h_{s}}}}\,\!$

${\overline {h_{s}}}=0.025km=25m\,\!$

সময়ের অগ্রগমন গণনা:

${\overline {h_{s}}}={\overline {v_{s}}}*{\overline {h_{t}}}=25=(60*1000/3600){\overline {h_{t}}}\,\!$

${\overline {h_{t}}}=1.5s\,\!$

নির্দিষ্ট পয়েন্ট দিয়ে দুটি গাড়ির মধ্যে সময়ের ব্যবধান হল ১.৫ সেকেন্ড।

চিন্তাগত প্রশ্ন

সমস্যা

মাইক্রোস্কোপিক ট্র্যাফিক প্রবাহ পৃথক যানবাহনের আচরণকে অনুকরণ করে যখন ম্যাক্রোস্কোপিক ট্র্যাফিক প্রবাহ সামগ্রিকভাবে ট্র্যাফিক স্ট্রিমের আচরণকে অনুকরণ করে। ধারণাগতভাবে, মনে হবে যে মাইক্রোস্কোপিক ট্র্যাফিক প্রবাহ আরও সঠিক হবে, কারণ এটি কেবল প্রবাহ বৈশিষ্ট্যের চেয়ে ড্রাইভারের আচরণের উপর ভিত্তি করে হবে। অনুমান করা হয় যে মাইক্রোস্কোপিক সিমুলেশনটি ড্রাইভারের আচরণের জন্য সত্যিকারের অ্যাকাউন্টে ক্যালিব্রেট করা যেতে পারে, একটি বড় নেটওয়ার্কের অনুকরণে প্রাথমিক ত্রুটি কী?

সমাধান

কম্পিউটার শক্তি। মাইক্রোস্কোপিক সিমুলেশনসহ একটি খুব বড় নেটওয়ার্ক অনুকরণ করার জন্য, মূল্যায়ন করা প্রয়োজন এমন যানবাহনের সংখ্যা খুব বেশি, যার জন্য প্রচুর কম্পিউটার মেমরি প্রয়োজন। বর্তমান কম্পিউটারগুলিতে একটি সময়মত ফ্যাশনে খুব বড় মাইক্রোস্কোপিক নেটওয়ার্কগুলি করার সমস্যা রয়েছে, তবে সম্ভবত ভবিষ্যতের অগ্রগতি এই সমস্যাটি দূর করবে।

নমুনা সমস্যা

• সমস্যা (সমাধান)

ভেরিয়েবল

• $d_{n}$= $n$^তম যানবাহনের দূরত্ব
• $t_{n}$= $n$^তম যানবাহনের ভ্রমণ সময়
• $v_{n}$= $n$^তম যানবাহনের গতি (বেগ)
• $h_{t,nm}$ = $n$ এবং $m$ গাড়ির মধ্যে সময় ব্যবধান
• $h_{s,nm}$ = $n$ এবং $m$ গাড়ির মধ্যে দূরত্ব ব্যবধান
• $q$ = একটি নির্দিষ্ট স্থান দিয়ে প্রবাহ (ঘন্টায় গাড়ির সংখ্যা)
• $N$ = গাড়ির সংখ্যা
• $t_{measured}$ = পরিমাপের সময়কাল (সেকেন্ডের সংখ্যা)
• $t$ = অতিক্রম করার সময়
• $k$ = ঘনত্ব (প্রতি কিলোমিটারে গাড়ির সংখ্যা)
• $L$ = রাস্তার অংশের দৈর্ঘ্য (কিলোমিটার)
• $v_{t}$ = সময়-মাধ্যম গতি
• $v_{s}$ = স্থান-মাধ্যম গতি
• $v_{f}$ = স্বাভাবিক গতি (যানজটহীন গতি)
• $k_{j}$ = জটলা ঘনত্ব
• $q_{m}$ = সর্বোচ্চ প্রবাহ (সর্বোচ্চ ঘন্টায় গাড়ির সংখ্যা)

Key Terms

• সময়-স্থান চিত্র
• প্রবাহ, গতি, ঘনত্ব
• ব্যবধান (স্থান ও সময়)
• স্থান-মাধ্যম গতি, সময়-মাধ্যম গতি
• ক্ষুদ্র পর্যবেক্ষণ (মাইক্রোস্কোপিক), বৃহৎ পর্যবেক্ষণ (ম্যাক্রোস্কোপিক)

অতিরিক্ত পাঠ্য

• ট্রাফিক প্রবাহ তত্ত্বের সংশোধিত মনোগ্রাফ (ইংরেজি)

ভিডিও

• ট্রাফিক প্রবাহ (ইংরেজি)

তথ্যসূত্র

• Banks, J.H. (1991). Two Capacity Phenomenon at Freeway Bottlenecks: A Basis for Ramp Metering? Transportation Research Record 1320, pp. 83–90.
• Banks, James H. (1992). “Freeway Speed-Flow-Concentration Relationships: More Evidence and Interpretations.” Transportation Research Record 1225:53-60.
• Cassidy, M.J. and R.L. Bertini (1999) Some Traffic Features at Freeway Bottlenecks. Transportation Research Part B Vol. 33, pp. 25–42
• Disbro, John E. and Frame, Michael. (1992). “Traffic Flow Theory and Chaotic Behavior.” Transportation Research Record. 1225: 109-115.
• Gerlough, Daniel L. and Huber, Matthew J. (1975). Traffic Flow Theory: A Monograph TRB Special Report 165. Transportation Research Board, Washington DC.
• Gilchrist, Robert S. and Fred L. Hall. (1992). “Three-Dimensional Relationships Among Traffic Flow Theory Variables.” Transportation Research Record. 1225:99-108.
• Hall, F.L. and K. Agyemang-Duah (1991). Freeway Capacity Drop and the Definition of Capacity. Transportation Research Record 1320, pp. 91–98
• Hall, Fred L., Hurdle, V. F., and Banks, James H. (1992). “A Synthesis of Recent Work on the Nature of Speed-Flow and Flow-Occupancy (or Density) Relationships on Freeways”. presented at TRB 71st Annual Meeting, Washington DC.
• Knoop, V.L., Hoogendoorn, S.P. and Van Zuylen, H.J. (2009) Empirical Differences between Time Mean Speed and Space Mean Speed. In Appert-Rolland, C., Chevoir, F., Gondret, P., Lassarre, S., Lebacque, J.-P. and Schreckenberg, M. (Eds.) Proceedings of Traffic and Granular Flow 07. pp. 351-356, Springer, New York
• Pensaud, B.N. and Hurdle, V. F. (1991). “Some New Data That Challenge Some Old Ideas About Speed-Flow Relationships.” Transportation Research Record. 1194: 191-8.
• Ross, Paul. (1991). “Some Properties of Macroscopic Traffic Models.” Transportation Research Record. 1194: 129-34.