ডিজিটাল সার্কিট/করডিক

CORDIC (যার পূর্ণরূপ COordinate Rotation DIgital Computer) সার্কিটটি বিভিন্ন সাধারণ গাণিতিক ফাংশন গণনা করতে ব্যবহৃত হয়। যেমন, ত্রিকোণমিতিক, হাইপারবোলিক, লগারিদমিক এবং সূচকীয় ফাংশন।

প্রয়োগ

একটি CORDIC শুধুমাত্র অ্যাডার এবং বিটশিফট ব্যবহার করে ফলাফল গণনা করে। এর সুবিধা হল এটি তুলনামূলকভাবে সহজ হার্ডওয়্যার ব্যবহার করে বাস্তবায়ন করা যায়।

পাওয়ার সিরিজ বা টেবিল লুকআপের মতো পদ্ধতিগুলো সাধারণত গুণফল সম্পাদনের প্রয়োজন হয়। যদি একটি হার্ডওয়্যার মাল্টিপ্লায়ার উপলব্ধ না থাকে, তবে CORDIC সাধারণত দ্রুত হয়। তবে যদি একটি মাল্টিপ্লায়ার ব্যবহার করা যায়, অন্য পদ্ধতিগুলি দ্রুত হতে পারে।

CORDICs বিভিন্নভাবে বাস্তবায়িত হতে পারে, যেমন একটি একক-পর্যায়ের পুনরাবৃত্তিমূলক পদ্ধতি, যা মাল্টিপ্লায়ার সার্কিটগুলির তুলনায় খুব কম গেট প্রয়োজন। এছাড়াও, CORDICs অনেক ফাংশন একই হার্ডওয়্যার দিয়ে গণনা করতে পারে, তাই তারা সেই প্রয়োগগুলির জন্য আদর্শ যেখানে গতি নয় বরং খরচ কমানোর উপর গুরুত্ব দেওয়া হয় (যেমন, FPGAs-এ গেট সংখ্যা কমিয়ে)। এই অগ্রাধিকারের একটি উদাহরণ হল পকেট ক্যালকুলেটর, যেখানে CORDICs খুব ঘন ঘন ব্যবহার করা হয়।

ইতিহাস

CORDIC প্রথম আবিষ্কার করেন J.E. Volder 1959 সালে Convair-এর অ্যারোইলেকট্রনিক্স বিভাগে। এটি B-58 Hustler বোম্বারের নেভিগেশনাল কম্পিউটারের জন্য ডিজাইন করা হয়েছিল, যা ত্রিকোণমিতিক ফাংশন গণনা করা একটি এনালগ রেজলভার প্রতিস্থাপন করতে ব্যবহৃত হত (সার্কুলার CORDIC)।

1971 সালে, J.S. Walther, Hewlett-Packard-এ, এই পদ্ধতিটি বাড়িয়ে হাইপারবোলিক ফাংশন, প্রাকৃতিক লগারিদম, প্রাকৃতিক সূচকীয়, গুণফল, ভাগ এবং বর্গমূল (লিনিয়ার CORDIC এবং হাইপারবোলিক CORDIC) গণনা করার জন্য প্রসারিত করেন।

2019 সালে, হাইপারবোলিক CORDIC ভিত্তিক, Yuanyong Luo এবং তার সহযোগীরা একটি Generalized Hyperbolic CORDIC (GH CORDIC) প্রস্তাব করেন, যা নির্দিষ্ট যেকোনো বেসের লগারিদম এবং সূচকীয় সরাসরি গণনা করতে সক্ষম। তাত্ত্বিকভাবে, হাইপারবোলিক CORDIC হল GH CORDIC-এর একটি বিশেষ ক্ষেত্রে।

সাধারণ ধারণা

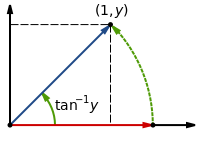
ভেক্টরের নিম্নলিখিত ঘূর্ণনগুলি বিবেচনা করুন:

(1, 0) থেকে শুরু করুন θ দ্বারা ঘূর্ণন করুন আমরা পাই (cosθ, sinθ)	(1, y) থেকে শুরু করুন ঘুরান যতক্ষণ না y = 0 হয় ঘূর্ণনটি হল tan−1y

যদি আমাদের একটি ভেক্টর ঘুরানোর জন্য একটি দক্ষ পদ্ধতি থাকে, আমরা সরাসরি sine, cosine এবং arctan ফাংশনগুলো নির্ণয় করতে পারি। তবে, একটি ইচ্ছেমত কোণ দ্বারা ঘূর্ণন করা সহজ নয় (তখন sine এবং cosine জানতেই হয়, যা ঠিক আমাদের কাছে নেই)। আমরা দুটি পদ্ধতি ব্যবহার করে এটিকে সহজ করি:

• ঘূর্ণন করার পরিবর্তে, আমরা "ছদ্মঘূর্ণন" করি, যা গণনা করা সহজ।
• নির্দিষ্ট কিছু কোণের α_i যোগফল থেকে ইচ্ছাকৃত কোণ θ তৈরি করি:

$\theta =\alpha _{1}+\alpha _{2}+\ldots +\alpha _{m}$

নীচের চিত্রটি একটি ভেক্টর R_i এর একটি কোণ a_i এর চারপাশে ঘূর্ণন এবং ছদ্মঘূর্ণন দেখায়:

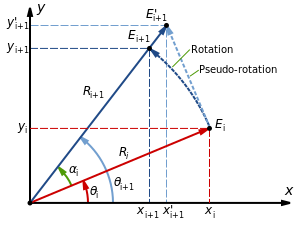
উৎসের চারপাশে একটি ঘূর্ণন নিম্নলিখিত স্থানাঙ্ক তৈরি করে:

$x_{i+1}=x_{i}\cos \alpha _{i}-y_{i}\sin \alpha _{i}$

$y_{i+1}=y_{i}\cos \alpha _{i}+x_{i}\sin \alpha _{i}$

$\theta _{i+1}=\theta _{i}+\alpha _{i}$

পরিচিতি পুনরাবৃত্ত করুন $\cos \theta \equiv 1{\Big /}{\sqrt {1+\tan ^{2}\theta }}$.

$x_{i+1}=\left(x_{i}-y_{i}\tan \alpha _{i}\right){\Big /}{\sqrt {1+\tan ^{2}\alpha _{i}}}$

$y_{i+1}=\left(y_{i}+x_{i}\tan \alpha _{i}\right){\Big /}{\sqrt {1+\tan ^{2}\alpha _{i}}}$

আমাদের কৌশল হবে $1{\Big /}{\sqrt {1+\tan ^{2}\alpha _{i}}}$ ফ্যাক্টরটি বাদ দেওয়া এবং $\tan \alpha _{i}$ দ্বারা গুণফল অপসারণ করা। একটি ছদ্মঘূর্ণন একটি ভিন্ন দৈর্ঘ্যের সাথে একটি ঘূর্ণিত ভেক্টরের সমান কোণ উত্পন্ন করে। প্রকৃতপক্ষে, ছদ্মঘূর্ণন দৈর্ঘ্য পরিবর্তন করে:

$R_{i+1}={\frac {R_{i}}{\cos \alpha _{i}}}=R_{i}{\sqrt {1+\tan ^{2}\alpha _{i}}}$

এখন আমরা নিম্নলিখিত স্থানাঙ্কগুলি পাই একটি ছদ্মঘূর্ণনের পর:

$x_{i+1}^{\prime }=\left(x_{i}-y_{i}\tan \alpha _{i}\right)$

$y_{i+1}^{\prime }=\left(y_{i}+x_{i}\tan \alpha _{i}\right)$

$\theta _{i+1}=\theta _{i}-\alpha _{i}$

ছদ্মঘূর্ণন সফলভাবে আমাদের দৈর্ঘ্য-ফ্যাক্টর অপসারণ করেছে, যা ব্যয়বহুল ভাগ অপারেশন প্রয়োজন হত। তবে, ভেক্টর n ছদ্মঘূর্ণনের একটি ক্রমে K ফ্যাক্টরে বৃদ্ধি পাবে:

$K=\prod _{i=0}^{n-1}{\sqrt {1+\tan ^{2}\alpha _{i}}}$

n ছদ্মঘূর্ণনের পরে স্থানাঙ্কগুলি হবে:

$x_{n}=K\left(x_{i}\cos \sum _{i=0}^{n-1}{\alpha _{i}}-y_{i}\sin \sum _{i=0}^{n-1}\alpha _{i}\right)$

$y_{n}=K\left(y_{i}\cos \sum _{i=0}^{n-1}{\alpha _{i}}+x_{i}\sin \sum _{i=0}^{n-1}\alpha _{i}\right)$

$\theta _{n}=\theta _{i}-\sum _{i=0}^{n-1}{\alpha _{i}}$

প্রথম তিনটি ছদ্মঘূর্ণন। লক্ষ্য করুন কিভাবে আমরা সঠিক কোণের দিকে এগোচ্ছি, θ

যদি কোণগুলো সবসময় একই সেট হয়, তাহলে K স্থির থাকে এবং পরে এটি সমন্বয় করা যায়। আমরা এই কোণগুলো নিম্নলিখিত দুটি মানদণ্ড অনুসারে নির্বাচন করি:

• আমাদের কোণগুলো এমনভাবে নির্বাচন করতে হবে যাতে যেকোনো কোণ তাদের যোগফল থেকে তৈরি করা যায়, যথাযথ চিহ্ন সহ।
• আমরা সব $\tan \alpha _{i}$ কে 2-এর ঘাত করে নেই, যাতে গুণফলটি একটি সাধারণ লজিক্যাল শিফট দিয়ে করা যায়।

ট্যাঙ্গেন্ট ফাংশনের [0, π/2] পরিসরে একটি একচেটিয়া বৃদ্ধিকারক প্রবণতা রয়েছে, তাই প্রদত্ত কোণের ট্যাঙ্গেন্ট সর্বদা অর্ধেক কোণের ট্যাঙ্গেন্টের দ্বিগুণের চেয়ে কম। এর মানে হল যে যদি আমরা কোণগুলি $\alpha _{i}=\tan ^{-1}2^{-i}$ করি, তাহলে আমরা উভয় মানদণ্ড পূরণ করতে পারি। মনে রাখবেন ট্যাঙ্গেন্ট ফাংশনটি বিজোড়, এর মানে অন্য দিকে ছদ্মঘূর্ণন করতে হলে, আপনাকে কেবল কোণের ট্যাঙ্গেন্ট বিয়োগ করতে হবে, যোগ করার পরিবর্তে।

i	αi = tan−1 (2−i)
	ডিগ্রি	রেডিয়ান
0	45.00	0.7854
1	26.57	0.4636
2	14.04	0.2450
3	7.13	0.1244
4	3.58	0.0624
5	1.79	0.0312
6	0.90	0.0160
7	0.45	0.0080
8	0.22	0.0040
9	0.11	0.0020

প্রক্রিয়ার i ধাপে, আমরা $d_{i}2^{-i}\,$ দ্বারা ছদ্মঘূর্ণন করি, যেখানে $d_{i}\,$ হল ঘূর্ণনের দিক (বা চিহ্ন), যা প্রতিটি ধাপে নির্বাচন করা হবে যাতে কোণটি চূড়ান্ত ঘূর্ণনের দিকে সংকোচন করতে পারে। উদাহরণস্বরূপ, 28° এর একটি ঘূর্ণন বিবেচনা করুন:

$28\approx 45.0-26.57+14.04-7.13+3.58-1.79+0.90-0.45+0.22+0.11$

$28\approx 27.91$

আমরা যত বেশি ধাপ নিই, ক্রমাগত ঘূর্ণন দ্বারা আমরা তত ভাল আনুমানিক করতে পারি। সুতরাং, আমাদের নিম্নলিখিত পুনরাবৃত্ত স্থানাঙ্ক গণনা আছে:

$x_{i+1}=x_{i}-d_{i}y_{i}2^{-i}$

$y_{i+1}=y_{i}+d_{i}x_{i}2^{-i}$

$\theta _{i+1}=\theta _{i}-d_{i}\alpha _{i}$

নির্দিষ্ট k বিটের নির্ভুলতা অর্জনের জন্য, k পুনরাবৃত্তির প্রয়োজন, কারণ $\tan ^{-1}2^{-i}\lessapprox 2^{-i}$, যা i বাড়ার সাথে সাথে সংকোচন

CORDIC ব্যবহারের পদ্ধতি

CORDIC বিভিন্ন ফাংশন গণনা করতে ব্যবহৃত হতে পারে। একটি CORDIC-এর তিনটি ইনপুট থাকে: x₀, y₀, এবং z₀। CORDIC-এ ইনপুটের উপর ভিত্তি করে, আউটপুট x_n, y_n, এবং z_n-এ বিভিন্ন ফলাফল তৈরি করা যায়।

ঘূর্ণন মোডে CORDIC ব্যবহার

$x_{i+1}=x_{i}-d_{i}y_{i}2^{-i}$ $y_{i+1}=y_{i}+d_{i}x_{i}2^{-i}$ $z_{i+1}=z_{i}-d_{i}\alpha _{i}$

$x_{n}=K\left(x_{0}\cos z_{0}-y_{0}\sin z_{0}\right)$ $y_{n}=K\left(y_{0}\cos z_{0}+x_{0}\sin z_{0}\right)$ $z_{n}=0$

z_n কে 0-তে সংকোচন করতে, $d_{i}={\mbox{sgn }}z_{i}$ বেছে নিন।

যদি আমরা x₀ = 1/K এবং y₀=0 দিয়ে শুরু করি, প্রক্রিয়া শেষে, আমরা পাই x_n=cos z₀ এবং y_n=sin z₀।

সঙ্কোচনের পরিসীমা হল $-99.7^{\circ }<z_{0}<99.7^{\circ }$ কারণ 99.7° সব কোণের তালিকার যোগফল।

ভেক্টরিং মোডে CORDIC ব্যবহার

$x_{i+1}=x_{i}-d_{i}y_{i}2^{-i}$ $y_{i+1}=y_{i}+d_{i}x_{i}2^{-i}$ $z_{i+1}=z_{i}-d_{i}\alpha _{i}$

$x_{n}=K{\sqrt {x^{2}+y^{2}}}$ $y_{n}=0$ $z_{n}=z_{0}+\tan ^{-1}\left(y_{0}/x_{0}\right)$

y_n কে 0-তে সংকোচন করতে, $d_{i}=-{\mbox{sgn }}(y_{i})$ বেছে নিন।

যদি আমরা x₀ = 1 এবং z₀ = 0 দিয়ে শুরু করি, আমরা পাই z_n=tan⁻¹y₀।

CORDIC এর বাস্তবায়ন

বিট-প্যারালেল, আনরোল্ড

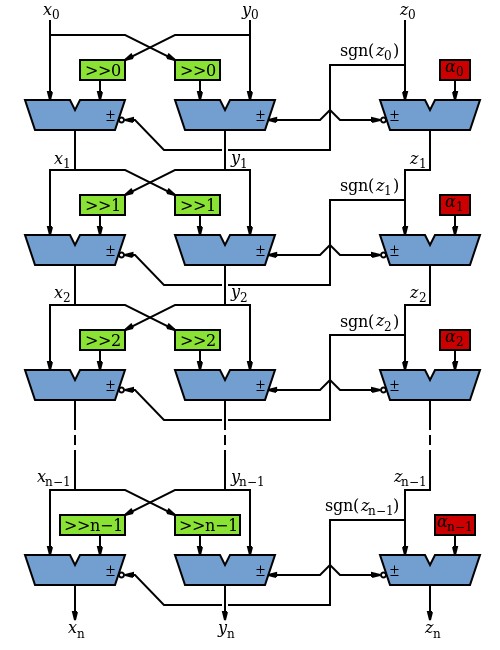
বিট-প্যারালেল, ইটারেটিভ

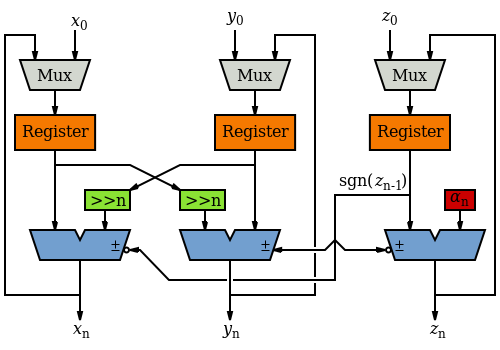
যদি উচ্চ গতি প্রয়োজন না হয়, এটি একটি একক অ্যাডার এবং একটি একক শিফটার দিয়ে বাস্তবায়িত করা যেতে পারে।

ইউনিভার্সাল কর্ডিক

একটি মূলক μ যোগ করে, আমরা লিনিয়ার এবং হাইপারবোলিক ফাংশনগুলির জন্য কর্ডিক ব্যবহার করতে পারি:

$x_{i+1}=x_{i}-\mu d_{i}y_{i}2^{-i}$

$y_{i+1}=y_{i}+d_{i}x_{i}2^{-i}$

$z_{i+1}=z_{i}-d_{i}\alpha _{i}$

ইউনিভার্সাল কর্ডিক বিবৃতির সারাংশ

$x_{i+1}=x_{i}-\mu d_{i}y_{i}2^{-i}$

$y_{i+1}=y_{i}+d_{i}x_{i}2^{-i}$

$z_{i+1}=z_{i}-d_{i}\alpha _{i}$

মোড	ঘূর্ণন	ভেক্টরিং
	$d_{i}={\mbox{sgn }}(z_{i}),\quad z\rightarrow 0$	$d_{i}=-{\mbox{sgn }}(y_{i}),\quad y\rightarrow 0$
বৃত্তাকার μ = 1 αi = tan−12−i
লিনিয়ার μ = 0 αi = 2−i
হাইপারবোলিক μ = -1 αi = tanh−12−i
হাইপারবোলিক মোডে, পুনরাবৃত্তি 4, 13, 40, 121, ..., j, 3j+1,... অবশ্যই পুনরাবৃত্তি করতে হবে। এর জন্য দেওয়া স্থিতিগুলি K' অনুযায়ী। K = 1.646760258121... 1/K = 0.607252935009... K' = 0.8281593609602... 1/K' = 1.207497067763...

সরাসরি গণনাযোগ্য ফাংশনসমূহ

$\sin z\,$	$\cos z\,$
$\tan ^{-1}z\,$	$\sinh z\,$
$\cosh z\,$	$\tanh ^{-1}z\,$
$y/x$	$xz$
$\tan ^{-1}(y/x)\,$	${\sqrt {x^{2}+y^{2}}}$
${\sqrt {x^{2}-y^{2}}}$	$e^{z}=\sinh z+\cosh z$

প্রত্যাশিত গণনাযোগ্য ফাংশনসমূহ

উপরের ফাংশনগুলির পাশাপাশি, পূর্ববর্তী গণনার ফলাফল সংযোজনে অন্যান্য ফাংশনগুলি উত্পন্ন করা যেতে পারে:

$\tan z={\frac {\sin z}{\cos z}}\,$	$\cos ^{-1}w=\tan ^{-1}{\frac {\sqrt {1-w^{2}}}{w}}$
$\tanh z={\frac {\sinh z}{\cosh z}}$	$\sin ^{-1}w=\tan ^{-1}{\frac {w}{\sqrt {1-w^{2}}}}$
$\ln w=2\tanh ^{-1}{\frac {w-1}{w+1}}$	$\log _{b}w={\ln w \over \ln b}$
$w^{t}=e^{t\ln w}$	$\cosh ^{-1}=\ln \left(w+{\sqrt {w^{2}-1}}\right)$
$\tan ^{-1}(y/x)\,$	$\sinh ^{-1}=\ln \left(w+{\sqrt {w^{2}+1}}\right)$
${\sqrt {x^{2}-y^{2}}}$	${\sqrt {w}}={\sqrt {(w+1/4)^{2}-(w-1/4)^{2}}}$